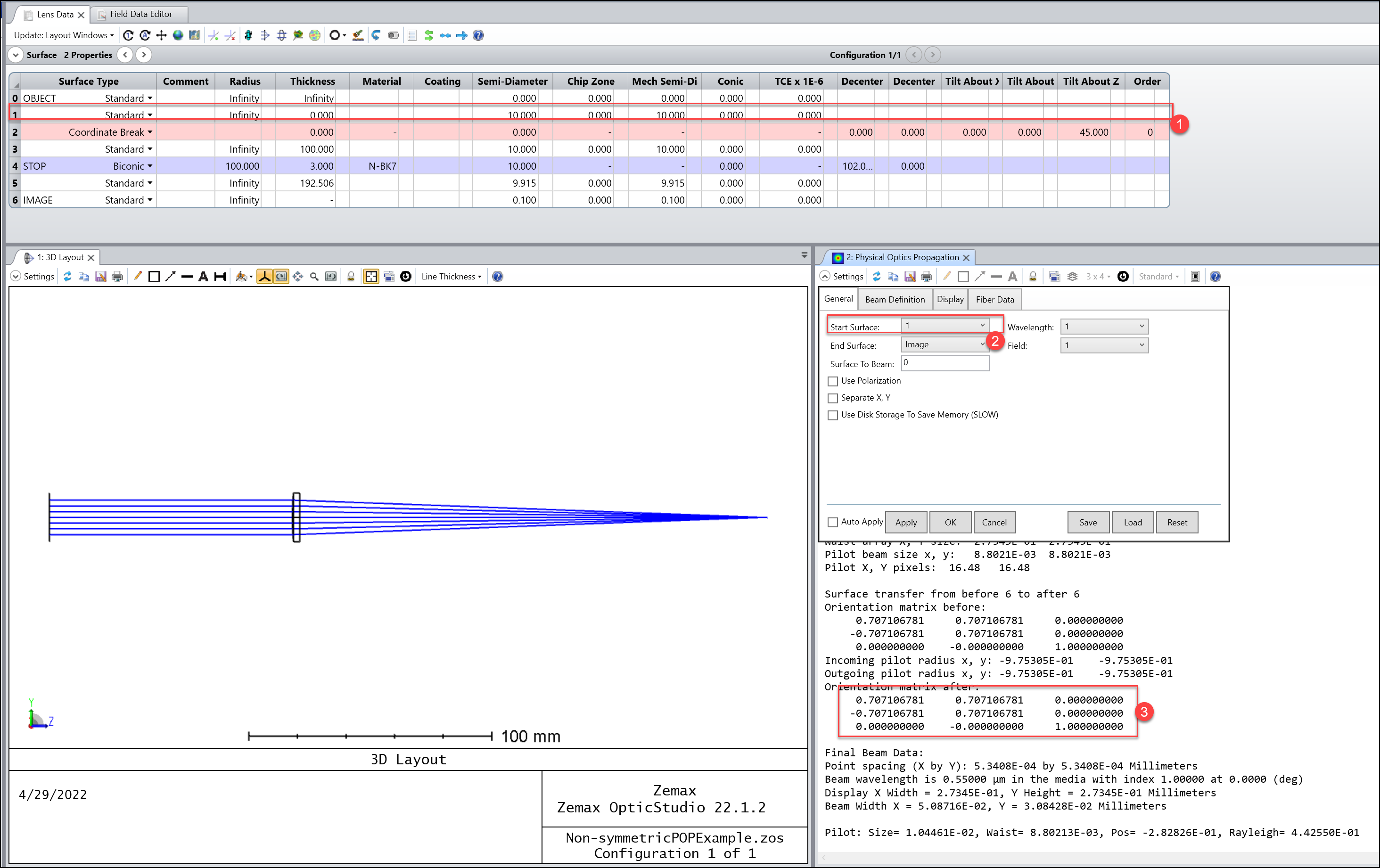
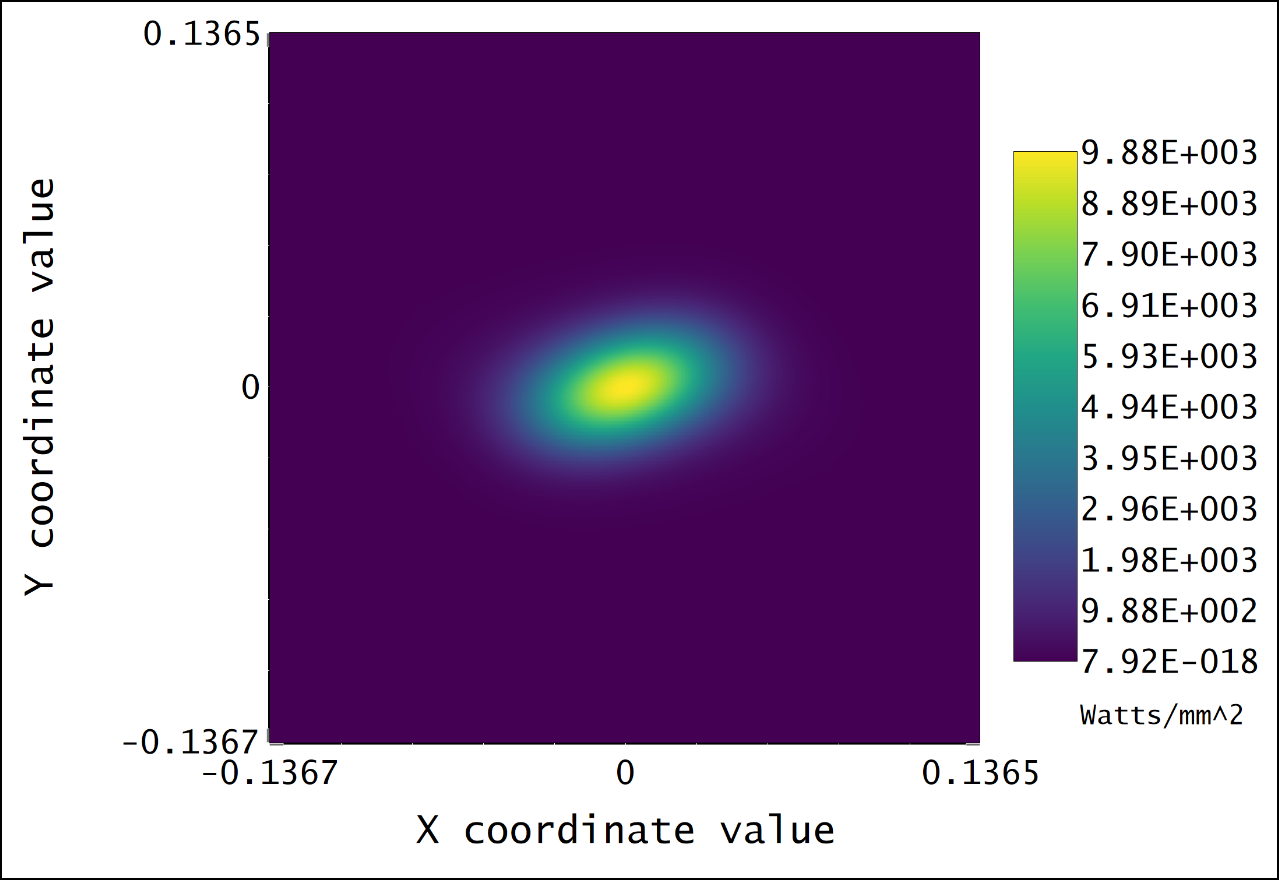
There are actually several possible answers depending on your files.
Some are because of misunderstanding to the POP result (mostly about the coordiante). Some are really diffraction effects and that can only show in POP and that's why you should use POP.
If it's complicated, you may still need to go support, but let's share experience here to help POP users! Hopefully, we can conver some most common questions here.
I will start by one or two below.