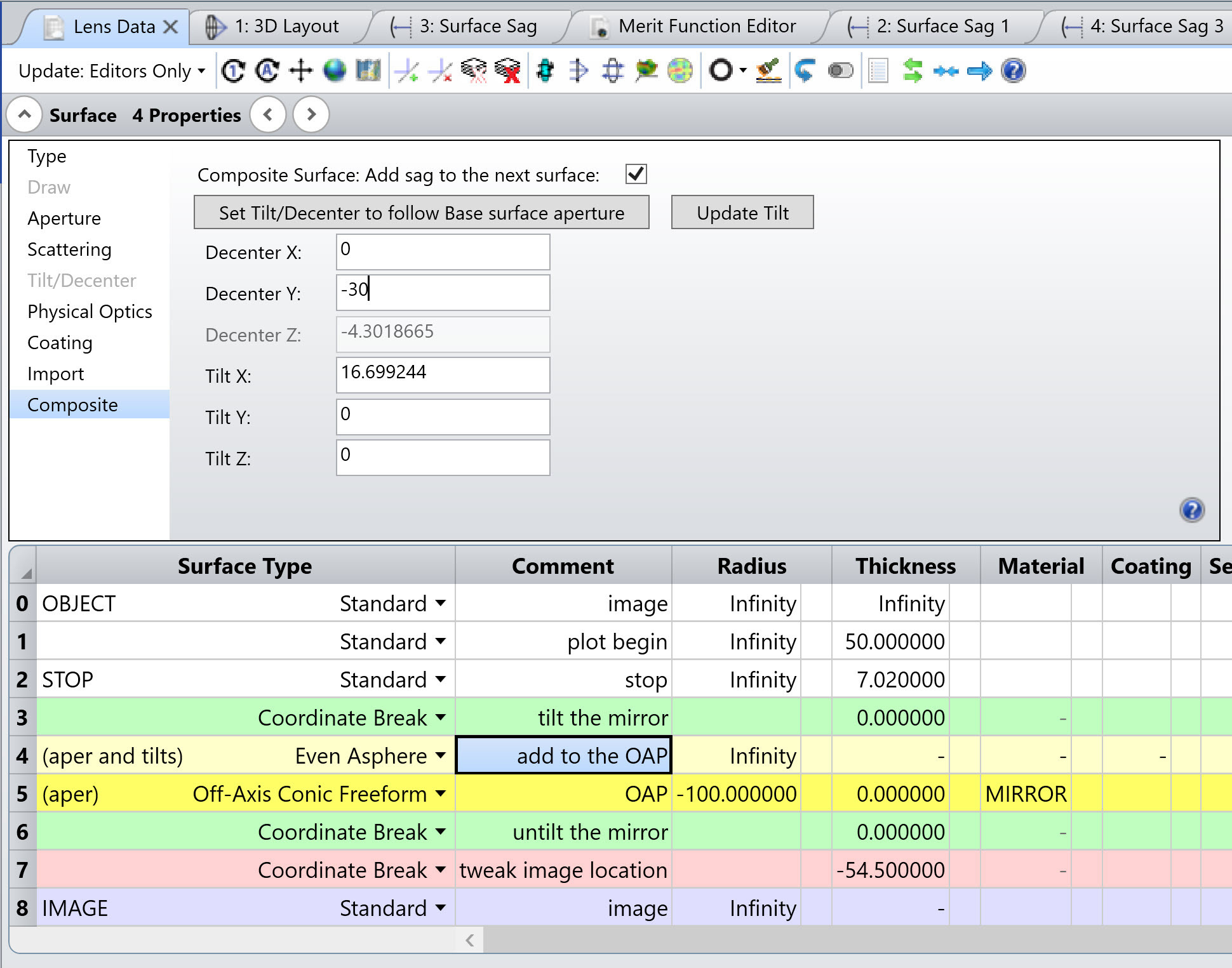
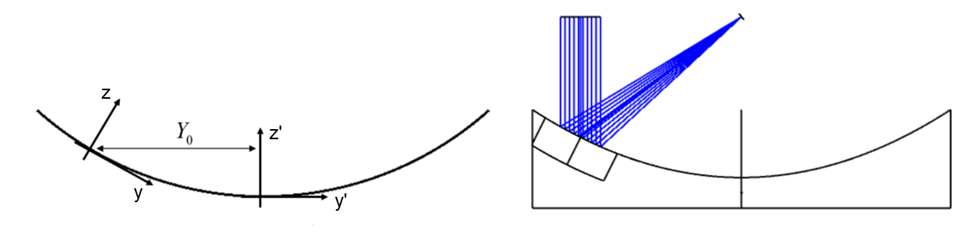
The Off-Axis Conic Freeform surface is the sum of an off-axis conic surface with freeform polynomial terms. The coordinate system for the surface is decentered and tilted to the center of the off-axis conic, as shown by the (y, z) coordinate system sketched below. Polynomial freeform terms are added to the surface at the center of the off-axis part. The edges of a mirror defined by this surface shape are parallel to the z axis.
The sag of the surface can be written as:
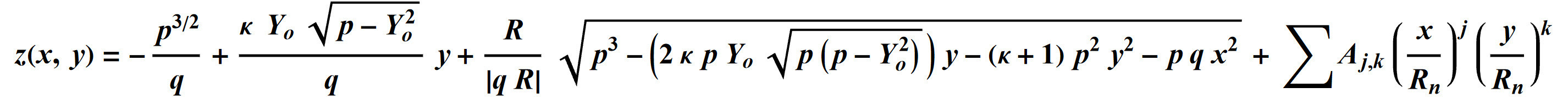
where:
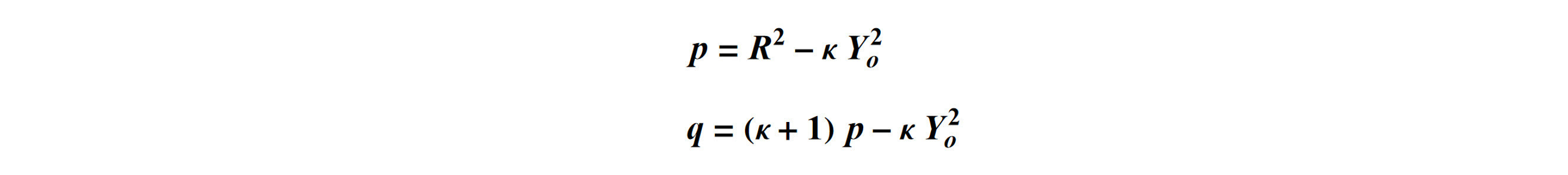
and R is the radius of curvature, k is the conic constant, Yo is the off-axis distance measured along the y axis of the on-axis conic, and Rn is the normalization radius for the freeform polynomial coefficients. The position coordinates x and y are in the off-axis coordinate system.
The freeform polynomial allows 230 terms, up to y20. The A00 term is omitted. The coefficients are arranged by increasing total power (j+k) and then by decreasing powers of x^j, as shown in the equation below. Note that the polynomial coefficients Aj,k are in lens units because the (x,y) coordinates are dimensionless.
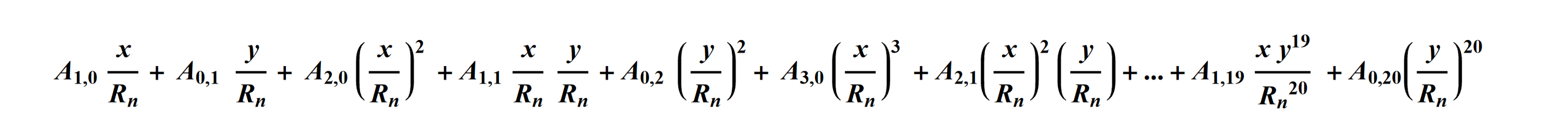
The freeform coefficients are specified in the Lens Data Editor beginning with parameter 13.
More details on the Off-Axis Conic Freeform surface derivation and design examples can be found in D. Reshidko, J. Sasian, "A method for the design of unsymmetrical optical systems using freeform surfaces," Proc. SPIE 10590, International Optical Design Conference 2017, 105900V (27 November 2017).