The polychromatic RMS wavefront error is calculated based on the following equation:
RMS polychromatic = sqrt(sum ((optical path difference for each ray of the pupil for each wavelength)^2 x weight of the ray)/ sum(weight of the ray)).
This means that the polychromatic RMS wavefront error is calculated for all wavelengths at the same time and for all the pupil.
For polychromatic results, the reference is the primary wavelength, so the wavefront error is calculated for each wavelength at the same time but with the reference set to the primary wavelength for each wavelength used. This means that for each wavelength, the rays are first propagated until the image plane, then the optical path length of each ray is recorded, then the rays are propagated back to the reference sphere defined by the chief ray at the primary wavelength, then path length of each ray is recorded again during this back-propagation, and finally the back-propagation path length is subtracted from the original path length.
In this way, the above formula includes the calculations for all wavelength as each weight of the rays already takes into account the different wavelengths and with their own potential weights too.
Another way to think about this is through the use of the OPDX Merit Function operands:

If we create a default merit function with the Optimization Wizard using the RMS Wavefront as criterion, then it will propagate the merit function with OPDX operands for rays at all wavelengths and for all the pupil with their own weights. If we delete certain OPDX operands to leave only specific field points (or build a default merit function with only one field defined), we can see the RMS Wavefront error for that specific field considering all wavelengths reported in the merit function value. The Merit Function is calculated based on the following formula:
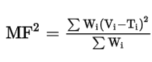
In this analogy, OPDX reports the optical path difference for the given ray in the value V, the target T is usually zero, and the weight W is the weight assigned to the ray. Thus, the OPD of the rays is squared and then the weighted average is calculated using the weights of the rays to calculate the square of the Merit Function value MF. This MF value equals the polychromatic RMS wavefront error.
As a simple example we can check these results in the Cooke triplet sample file from the \Documents\Zemax\Samples\Sequential\Objectives folder. The polychromatic RMS wavefront error is denoted by the black line in the RMS vs Field plot:
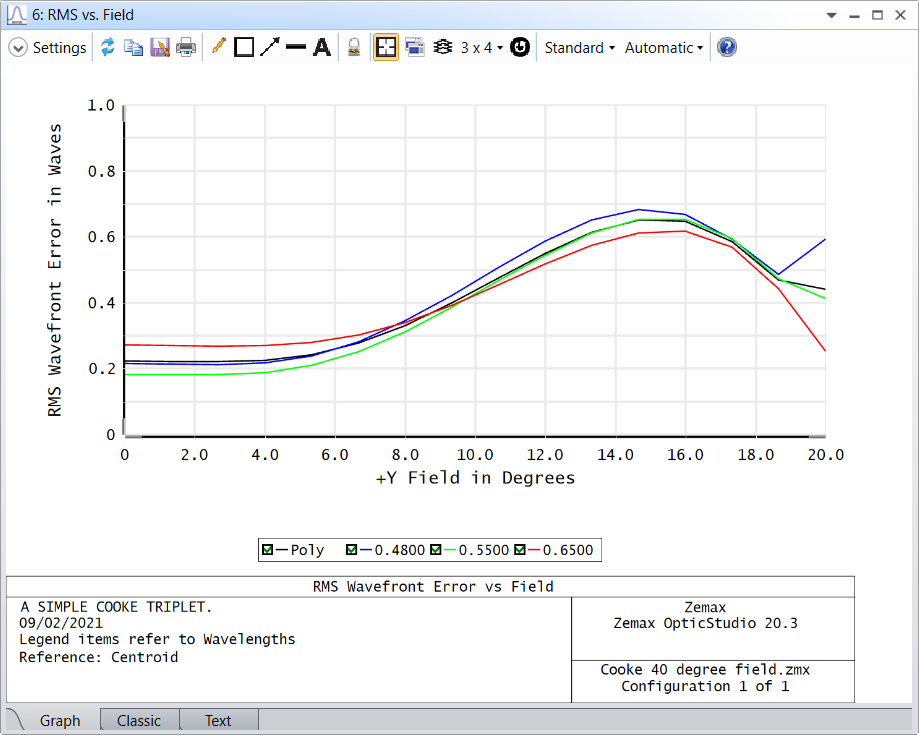
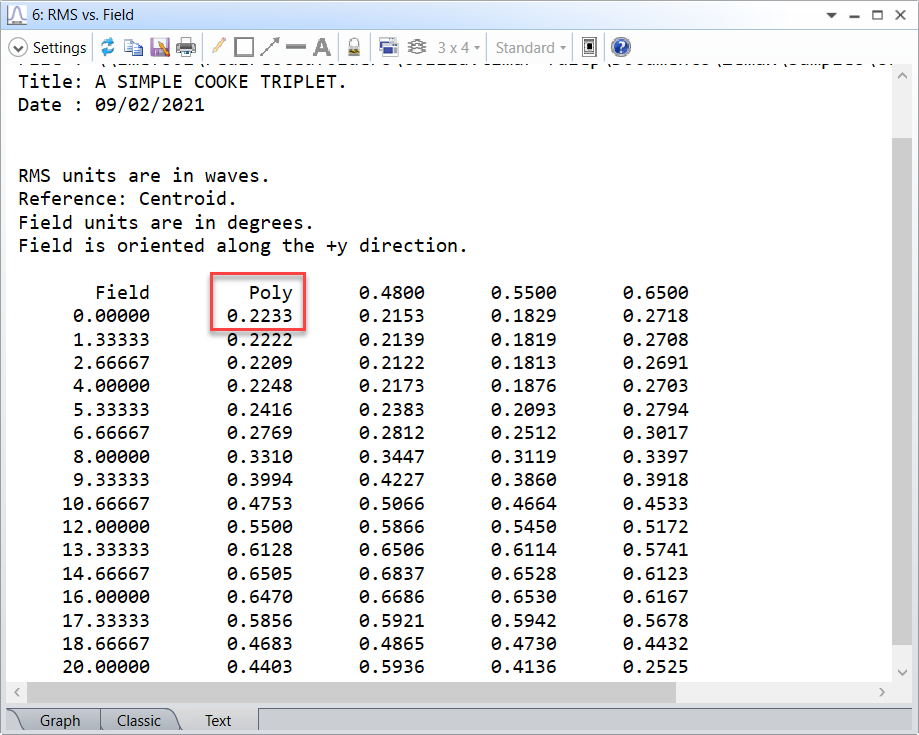
The Text window reports the numeric results too, and for the on-axis central field it is 0.2233 waves.
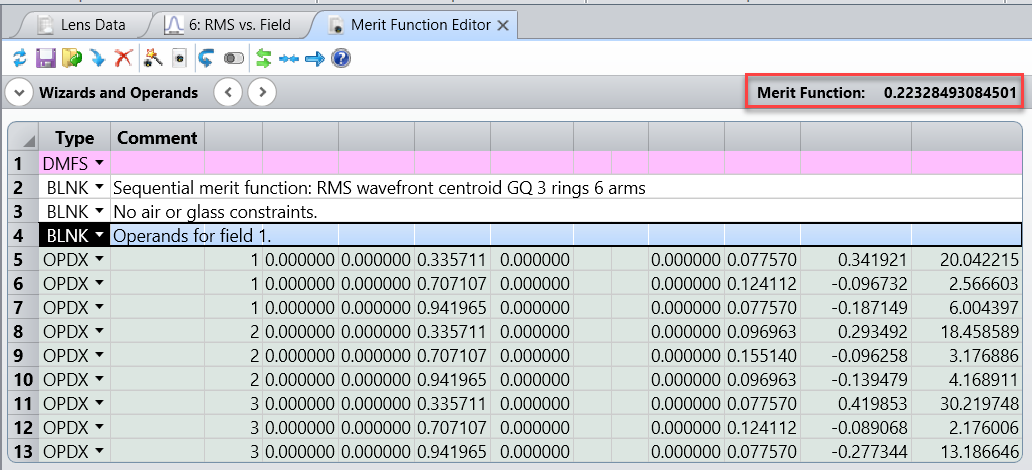
If we generate a default RMS Wavefront merit function using only the on-axis field point, we get back the same result reported as the Merit Function value:
The RMS wavefront error of the individual wavelengths is not used in the calculation of the polychromatic RMS wavefront error. Instead, OpticStudio uses the raw data of the individual rays, and the polychromatic RMS wavefront error is calculated directly from these raw data. Thus, it is based on the optical path difference of each ray of the pupil at each wavelength.
As the monochromatic RMS wavefront error is always referenced to the actual wavelength, while in case polychromatic calculations a common reference is needed and used, i.e. the primary wavelength, this means that in general the polychromatic RMS wavefront error can be larger than the average of the monochromatic RMS values.






