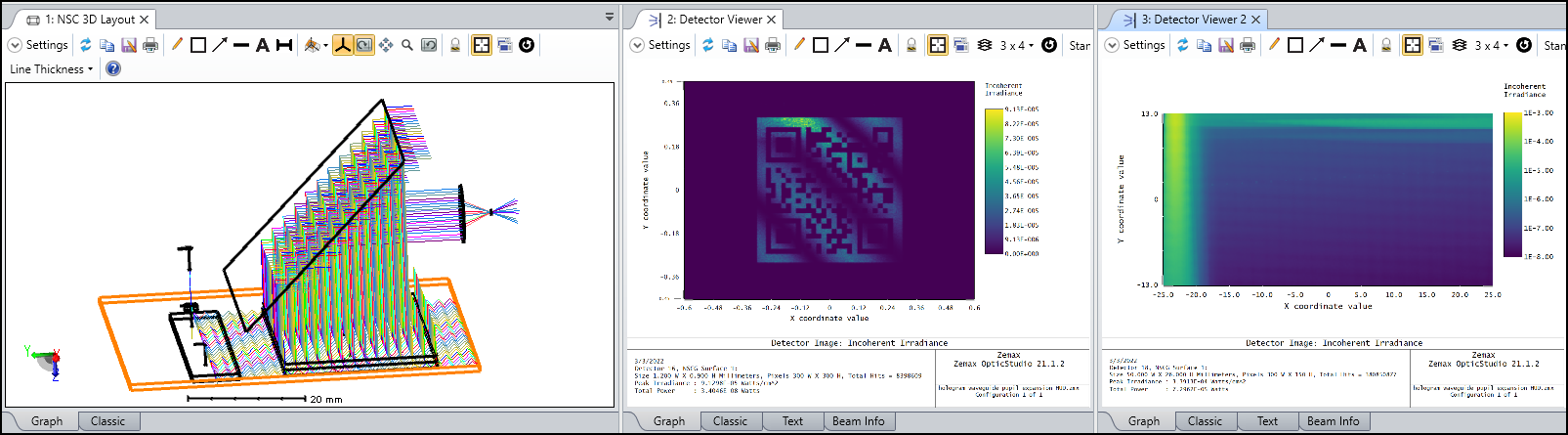
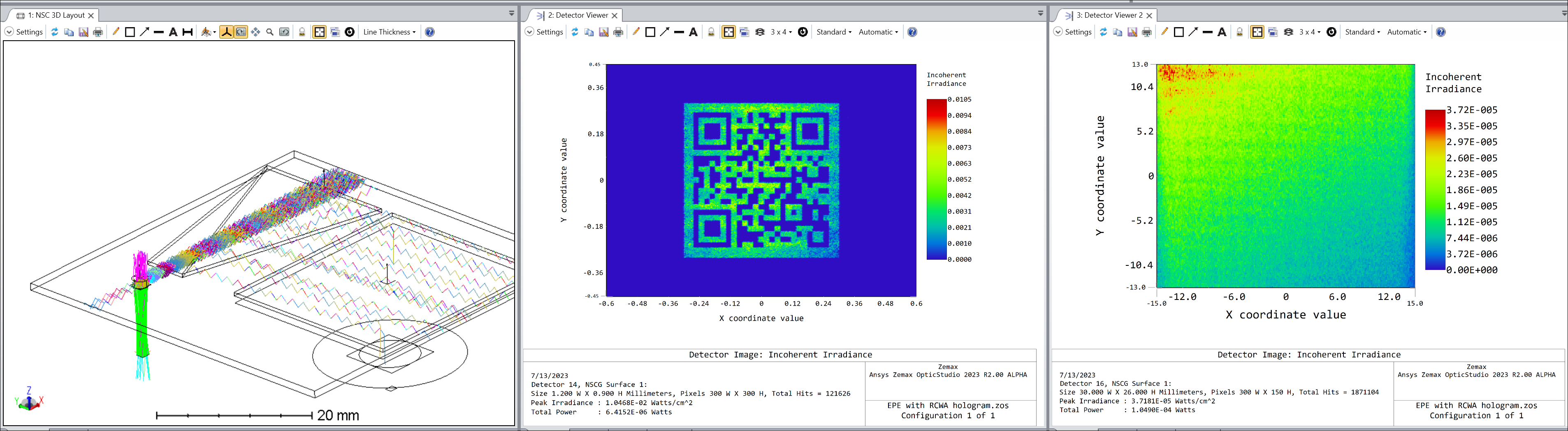
In the following article, we introduced how to build an EPE based on surface-relief grating (SRG). However, this does not work for holographic gratings.
The current available Kogelnik model in OpticStudio cannot be used for EPE waveguide. Here we will explain why and provide a workaround DLL.
Note this is based on assumptions and the result could be inaccurate.
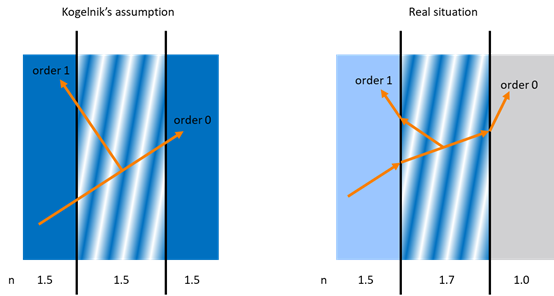
In Kogelnik’s method, it assumes, as below, that the refractive index of the hologram itself and its environment are same. Even after the hologram fringes are developed, the average refractive index is still same.
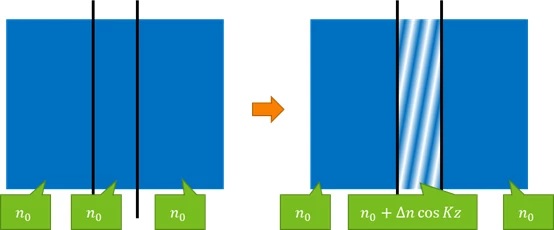
However, in reality, the refractive index from the environment is different.
For example, we might have a hologram, with average refractive index of n0 = 1.5, coated on a glass substrate, with refractive index of n1 = 1.7. And the other side is AIR, with refractive index of n2 = 1.0.
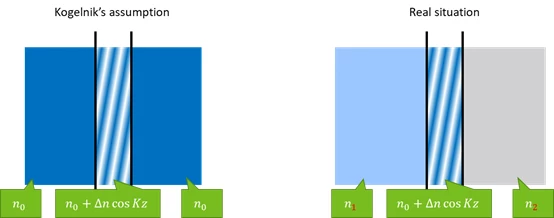
In real situation, the ray behavior will be a little different. You can imagine the rays need to be refracted at the boundary as shown in the right picture below.
Note this it NOT exactly what happens in the hologram, but it’s a very intuitive way to explain. And it’s roughly correct.
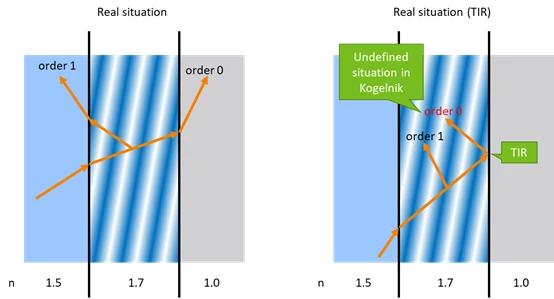
So now the problem is this means sometimes the ray can see TIR condition and can not leave the hologram zone. You can see the order 0 in the right side in following picture.
In Kogelnik method, the power of this TIR ray is undefined. In the DLL and the native implementation in current OpticStudio, we simply stop tracing rays in this case.
Normally, the holographic grating is rarely used in this way and we won’t have problems. However, for EPE waveguide applications, this is a very common case.
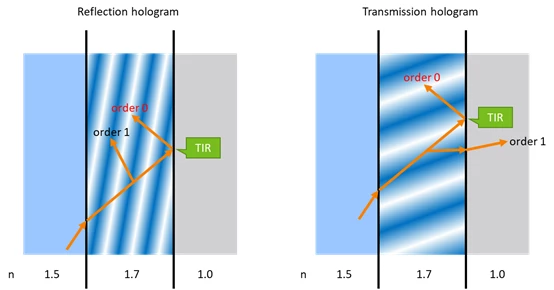
Note, not only reflection hologram, this can happen to transmission hologram too.
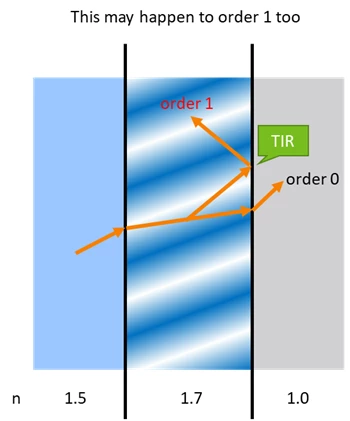
And it could happen to order 1 too.
In attached ZAR file, we have used two assumptions to make the DLL also working for TIR conditions. Note users should set the waveguide mode to non zero in order to turn the feature on. The two assumptions are:
- If the order 1 ray does not exist, the order 0 takes all power.
- If the order 0 ray encounters TIR condition, it goes reflection direction.
The system works as below.
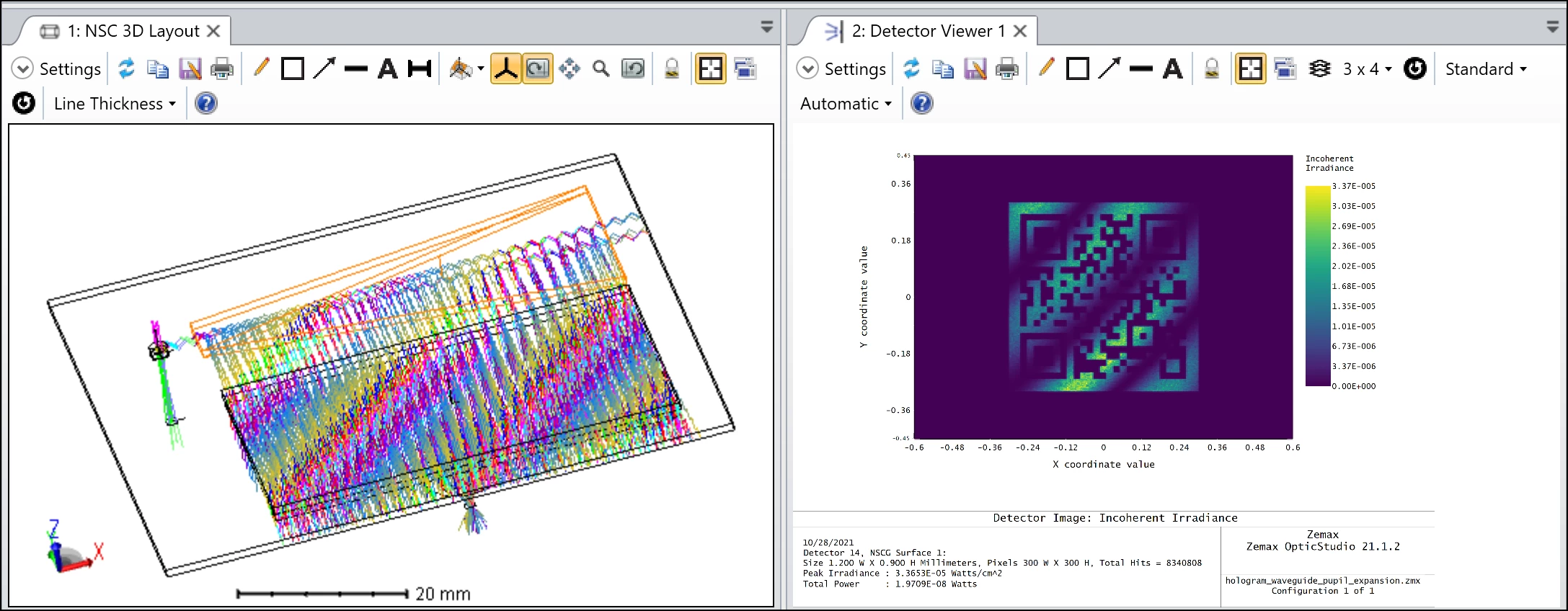
By opening this ZAR file, the workaround DLL will be extracted to the correct folder.
Note this DLL has a few restrictions:
- The DLL is only a workaround and it works with some assumptions. The result could be inaccurate. Readers should check the theories and the assumptions.
- This DLL is locked to subscription license.
For more general information about Kogelnik model in OpticStudio, readers can refer to the following article:
Simulating diffraction efficiency of a volume holographic grating using Kogelnik’s method