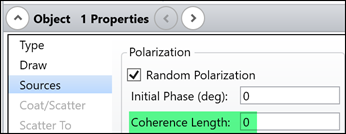
In OpticStudio, an option is available for assigning Coherence Length to a source as shown below. This works based on randomizing the wavelength of each ray.
In this post, an another method is demonstrated for simulating coherence length. In this method, it’s assume light with different wavelength cannot interfere. In other words, the interference pattern of a multi-wavelength source is the incoherent sum of the interference pattern of each wavelength themselves.
In fact, light with different wavelength could interfere. However, the interference pattern cannot be detected because the pattern changes with very high frequency and vanishes when sensor averages it over time. The following picture explains it.

To calculate the interference pattern of each wavelength and incoherently sum them, we need to do it manually. Here we provide a simple case and an ZOS-API code to demonstrate how to do it.
To see how it works, users just need to open the attached ZAR file, turn on Interactive Extension Mode, and run the attached MATLAB code.
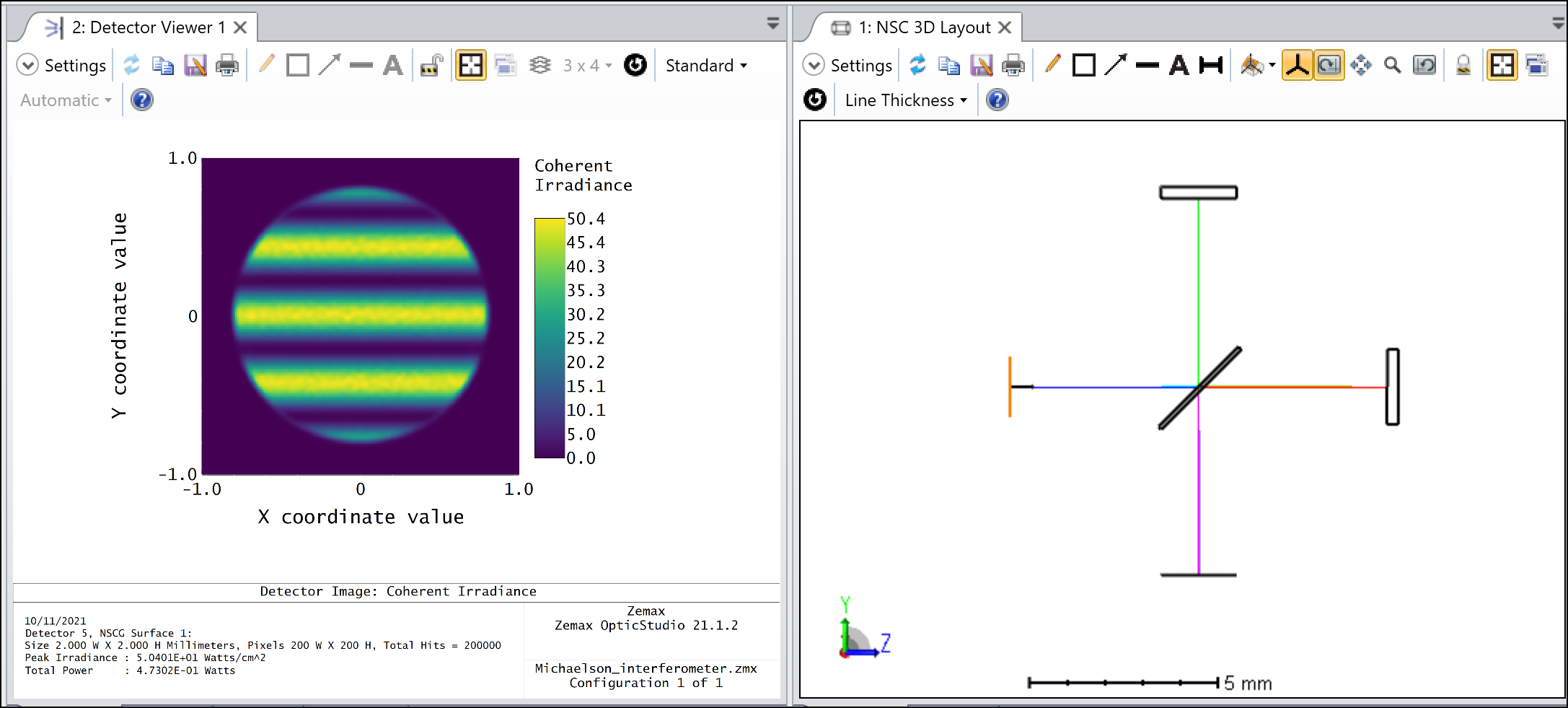
The system in the ZAR file is as below. It’s a Michaelson interferometer.
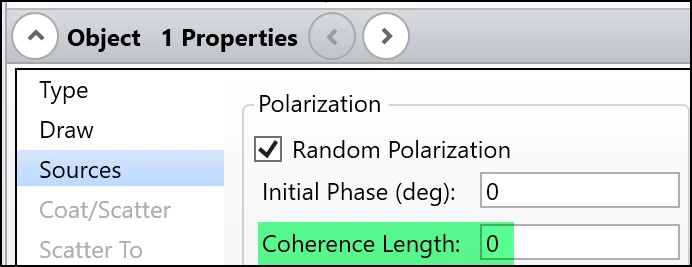
Note, in this method, we don’t use the Coherence Length settings. We just set it to zero to turn the function off.
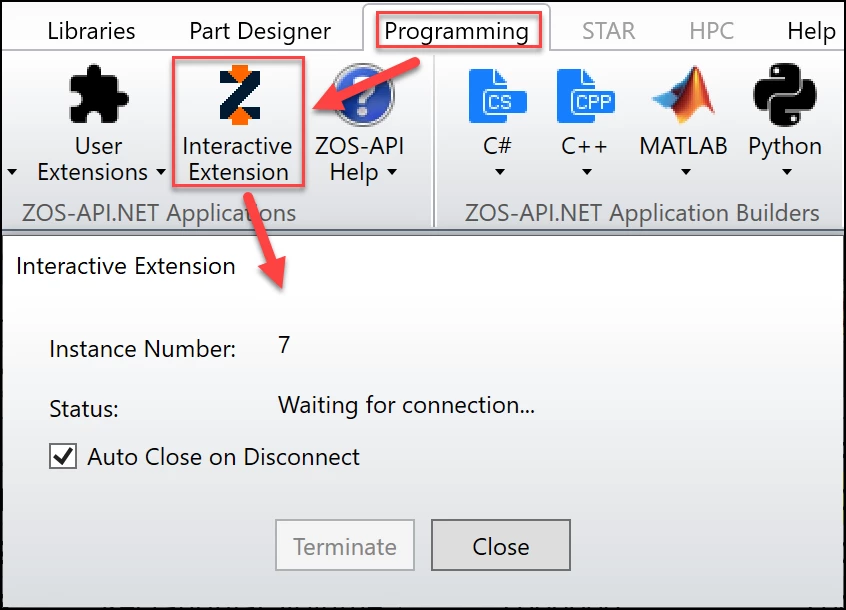
The Interactive Extension Mode can be turned on as shown below.
If you use this example code with your own system, you at least should check and modify the following 6 variables.
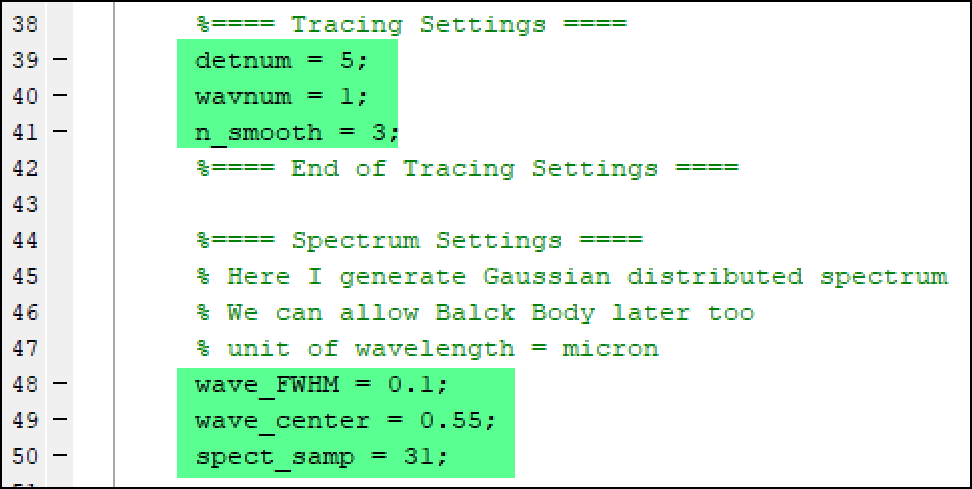
1. detnum is the object # of the Detector Rectangle you want to observe the interference pattern.
2. wavenum is the Wavenumber you used for your source parameter. It’s suggested you exactly specify this instead of leave it “0”.

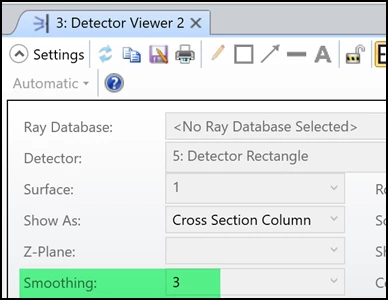
3. n_smooth works same as the Smooth parameter you see in the Detector Viewer.
4. wave_FWHM is the full width at half maximum of the Gaussian distributed source spectrum.
5. wave_center is the center of the Gaussian distributed source spectrum.
6. spect_samp is the sampling points you want to use to sample the spectrum. The more the accurate but slower the ray-tracing.
Here is the tracing result.
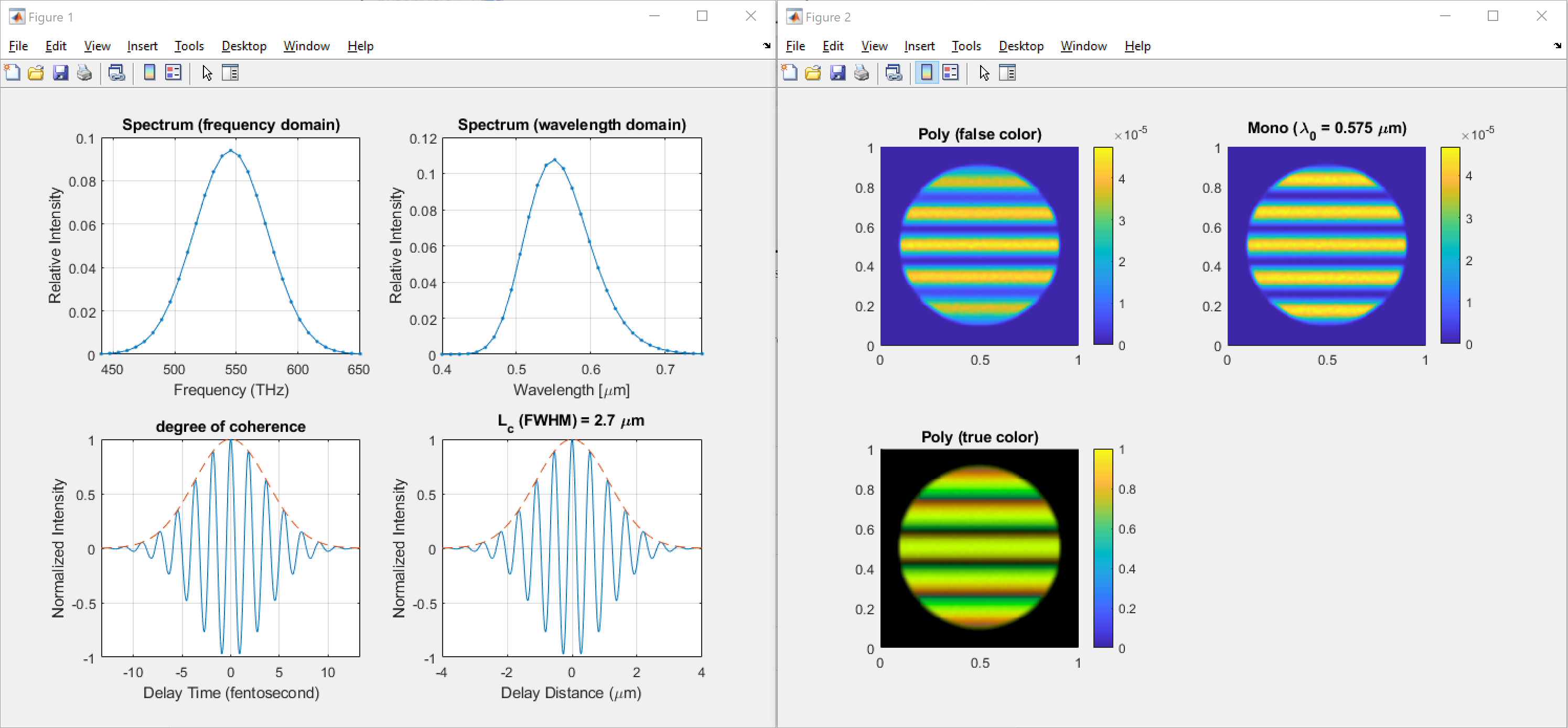
Enjoy it!







