Dear Zemax Community,

I am using a toroidal surface in my system to mimic a deformable surface which can have various sphere and cylinder power. I am tuning the radius of this curvature according to the desired sphere power using the simple formula:

R=delta_n/P_sphere 

Zemax is computing the EFFL of my system and gives me consistent results so I’m happy so far (100mm efl for a psherical power of 10D).

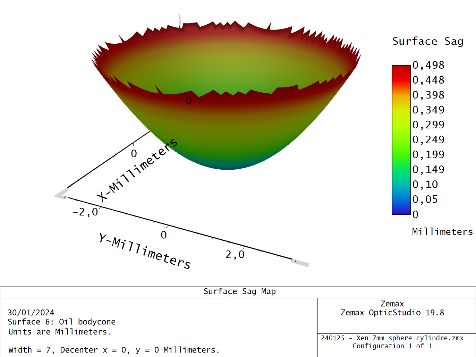
Now I am computing the radius of rotation of my toroidal surface using the sum of sphere power and cylinder power. If the cylinder power power is 0D, I get a nice spherical cap corresponding to my spherical power alone:

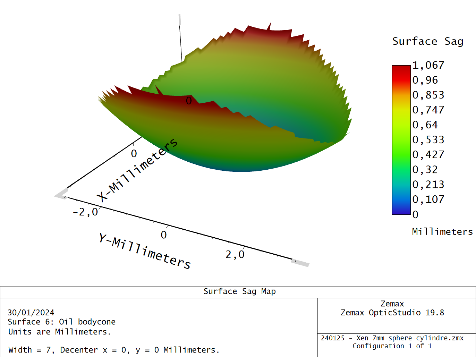
When I change the cylinder power to a non-zero value, the surface deforms and I get for 10D of cylinder:

Now, I would like to double check if my reasoning is okay by computing the spherical and cylinder power from the Zernike coefficients. Here is where my troubles begin...

I extract the Zernike Fringe Coefficients in the image plane:
Field                        :    0,0000 (deg)
Wavelength                   :    0,5880 µm

Z   1       76,29008061    :     1
Z   2       -0,00000003    :     (p) * COS (A)
Z   3       -0,00000006    :     (p) * SIN (A)
Z   4       75,47240005    :     (2p^2 - 1)
Z   5       53,52459851    :     (p^2) * COS (2A)
Z   6        0,00000002    :     (p^2) * SIN (2A)
Z   7        0,00000000    :     (3p^2 - 2) p * COS (A)
Z   8       -0,00000002    :     (3p^2 - 2) p * SIN (A)
Z   9       -0,75663782    :     (6p^4 - 6p^2 + 1)

and I wonder which formula to use to get back to my spherical power and cynlinder power.

The wavelength i’m using is 588nm and the pupil radius is 3.5mm.

Thanks for your help