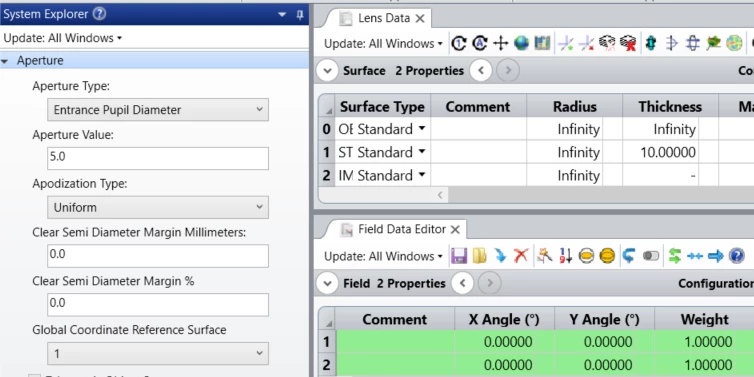
Let’s say my optical setup only has a circular aperture of radius R, with a blackbody surface that overfills this aperture, and image surface at distance h from aperture.
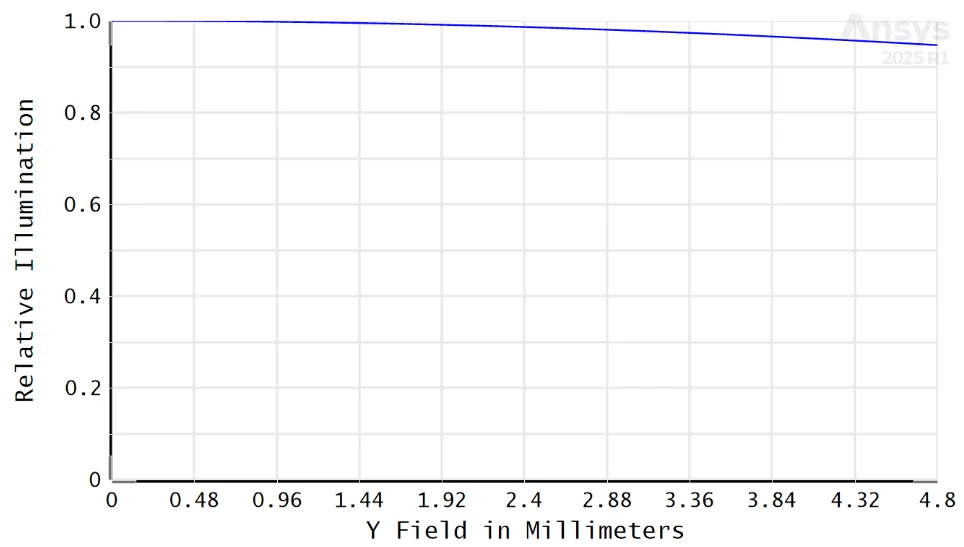
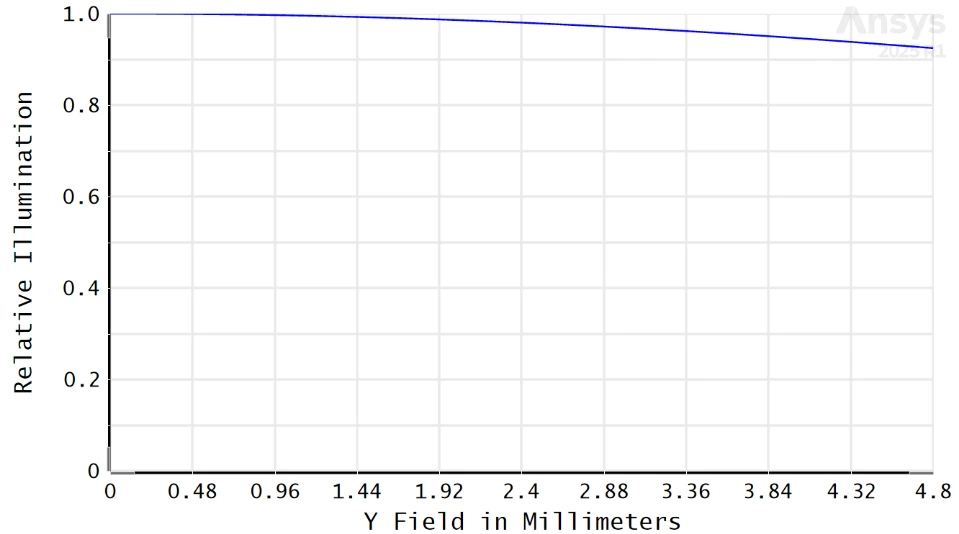
In a real setup, the image given by a sensor is an almost-flat image, with just a small roll-off from the center towards the edges often called “cos4” effect.
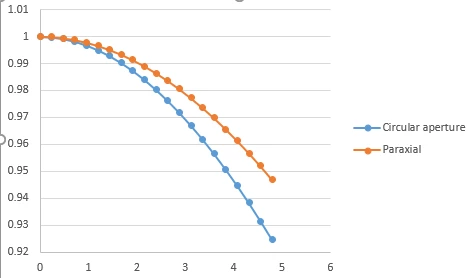
My question is : is the Relative illumination tool, and the associated effective F number, well adapted for computing such roll-off profile ?
note that the doc states about : “The computation method assumes [...] the image surface is a reasonably good conjugate (that is, an image) of the object surface”, so it does not seems to apply. On the other hand, the doc also states “The relative illumination is computed by integration of the effective area of the exit pupil as seen from the image point(s)” which seems like the right thing.