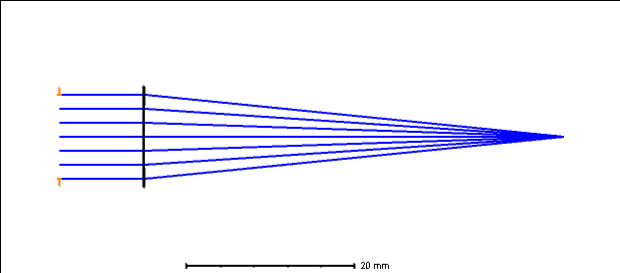
Simplest possible non-sequential file - 3 objects:
- Source Ellipse (10mm in X and Y, collimated, 1E6 analysis rays),
- NSC Paraxial Lens (X and Y half width = -6mm, X/Y focal length set to 50mm),
- Detector Rectangle (X and Y = 0.02mm, 100x100 pixels, with Data Type=1, PSF Wave # = 1)
The detector is located 50mm from the paraxial lens, so it is at focus. However, the above parameters just give gibberish rather than a PSF pattern. What am I doing wrong? How can I get an NSC paraxial lens to form a coherent irradiance diffraction pattern on a rectangular detector? Is the NSC Paraxial Lens object incapable of doing this?
Thanks, Mike