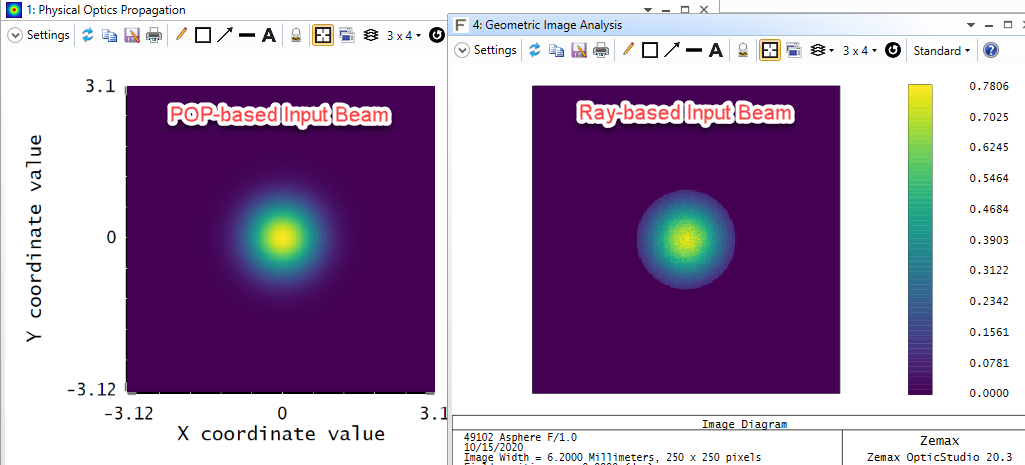
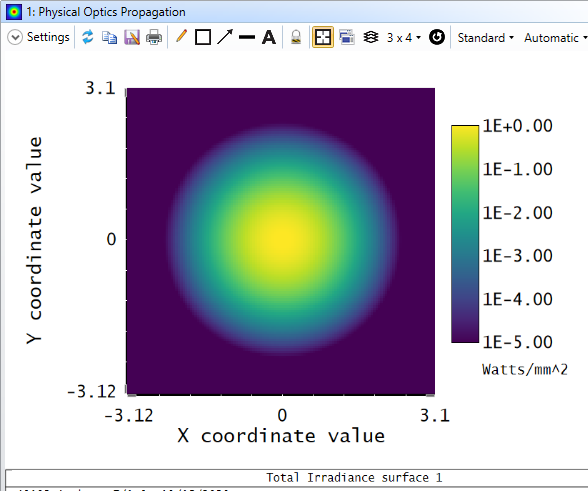
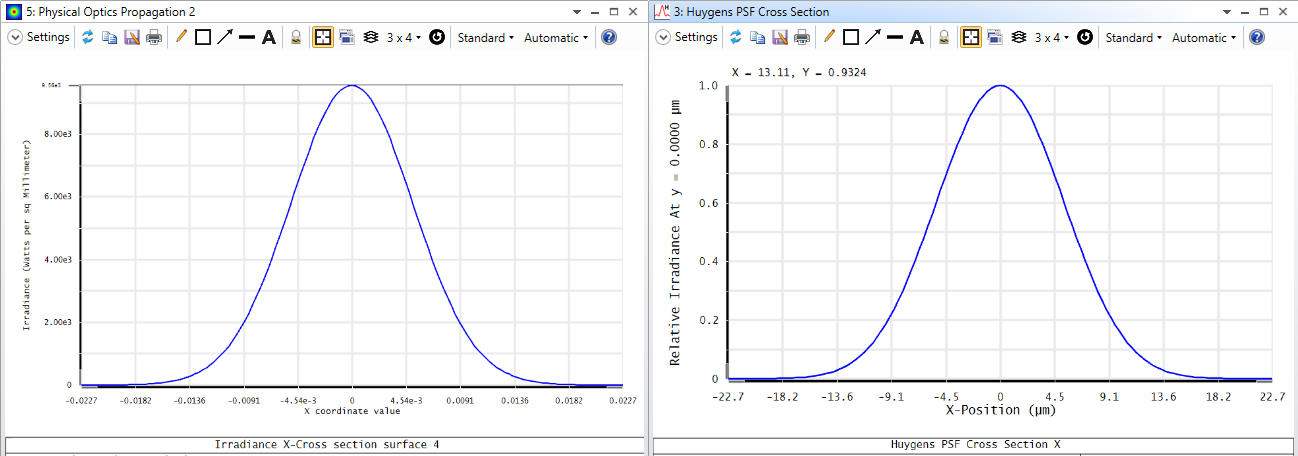
Hi everyone,
I am trying to compare the focal spot size and intensity between two different GRIN lenses, whose refractive index profile has been designed using Gradient 2. However, I am having some problems in quantifying the effect on the focal spot, that I try to articulate here:
1) Using the Quick Focus feature (spot size radial) results in unexpected results, as the one shown below:
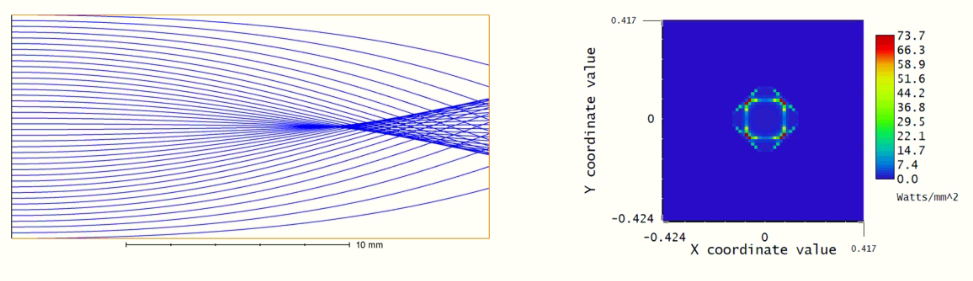
Is there another way to find the optimal focus without performing a manual scanning of the image plane?
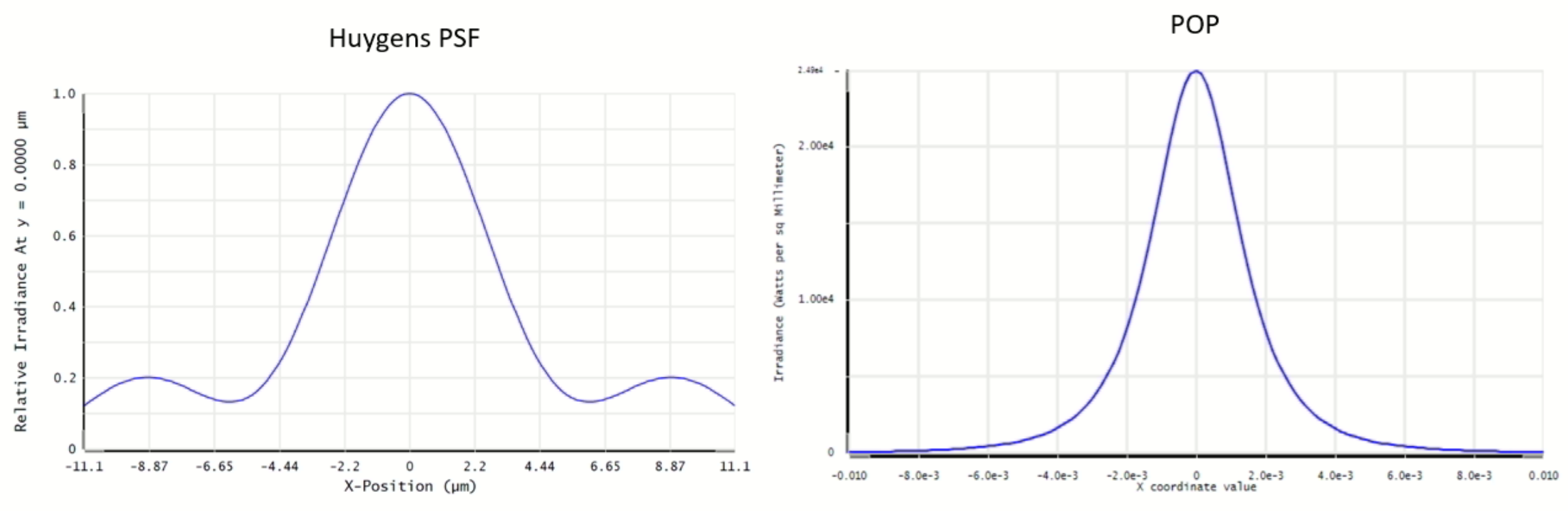
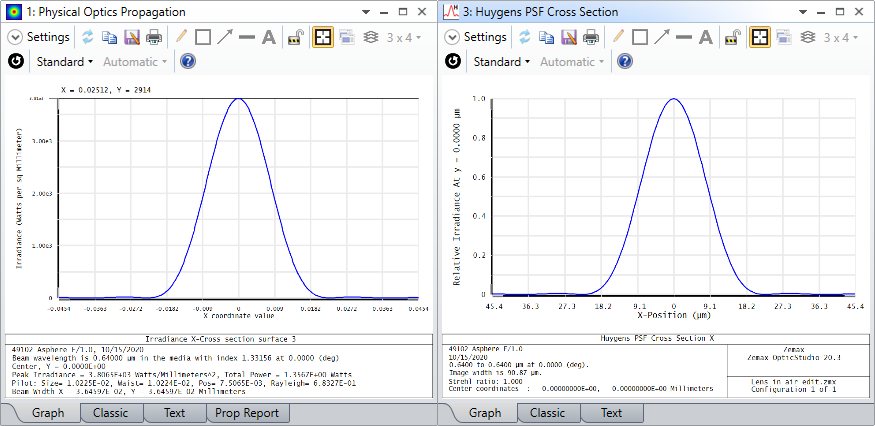
2) The scope of the simulation is to visualize a 2D image of the irradiance at the focal spot. I've read somewhere that for GRIN profiles, the results in terms of irradiance when using Huygens PSF and POP should match. Is it correct? I performed multiple attempts in POP (after scanning the image plane manually to find a result that does make sense), using even the max X and Y sampling, but the results are always different.Therefore, my question is: should I trust the PSF or POP results?
3) I noticed that by increasing the X and Y sampling in the POP simulations, the irradiance changes in terms of intensity and spatial distribution. Usually, a simulation can be defined as converged if increasing the resolution/sampling does not produce any variation in the results. However, here I cannot increase the sampling to more than 16k. Is there another way to check if the simulation converged?
Thanks in advance for your help!