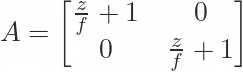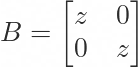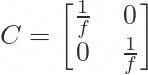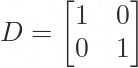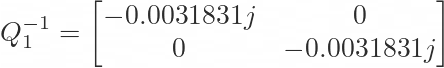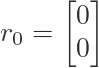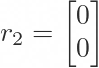Hey
Quick question about your VCSEL work, maybe primarily about Case 3 (I didn’t want to detract from the answer your already gave). I assume you validate your final sequential model with POP, but have you come across cases where POP doesn’t work and needed to use CodeV’s BSP (Gaussian Beam Decomposition)? BSP/GBD can be much quicker than POP with the added benefit that you can simulate free-space divergence in non-sequential mode. However, from my understanding BSP/GBD has some issues with sampling/MSF ringing and sometimes has issues with accurately calculating intensity.
I think Zemax should add GBD as another tool that can validate diffraction systems like this, but I haven’t looked into this too much. There are dozens of resources talking about GBD which could be a good starting point for Zemax to look into:
https://arxiv.org/pdf/2106.09162.pdf
https://poppy-optics.readthedocs.io/en/latest/
Curious about everyone’s thoughts.