I have implemented a simple system composed of:
- Diode Source with 2deg divergence in x and y;
- Diffuser implemnted with cylinder volume with a single scaterring surface following a gaussian model with sigma = 0.27
- Polar detector to monitor the angular distribution of energy after the diffuser in the range -90, +90 deg;

After exporting the detector data using the ”Detector Viewer", I have fitted the data points with the gaussian model described in the Help documentation: BSDF = A*exp(-x**2 / sigma ** 2):
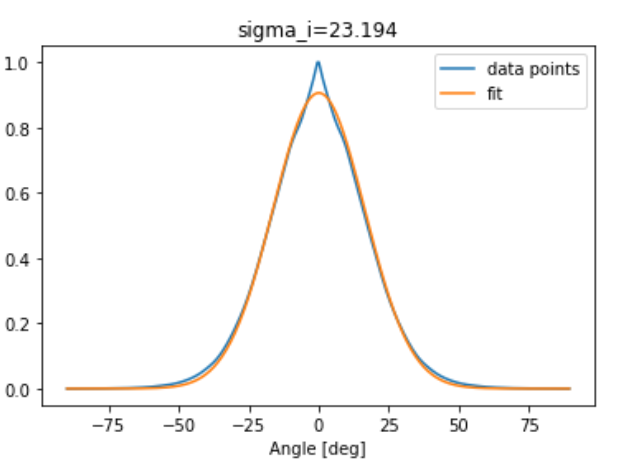
The value of the fitted sigma (sigma_i = 23.194) has nothing to do with the specified sigma of the diffuser (sigma = 0.27), which tells me that my interpretation of the scattering model is wrong. Where does the discrepancy come from?



