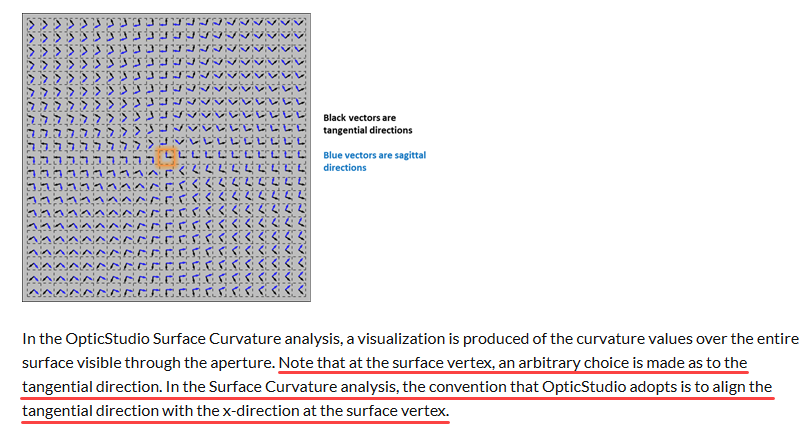
In the Surface Curvature analysis, the convention that OpticStudio adopts is to align the tangential direction with the x-direction at the surface vertex.
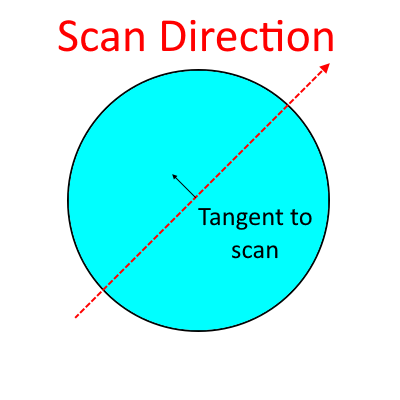
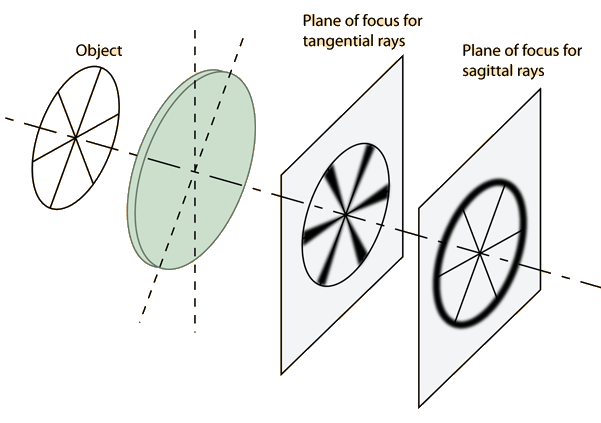
This statement is true and of course the choice is arbitrary, but it seems to me this convention is 90 degrees at odds with where we use the term tangential elsewhere. The surface curvature data is independent of ray tracing, but when doing raytracing the convention OS uses is that tangential is along the y-axis.
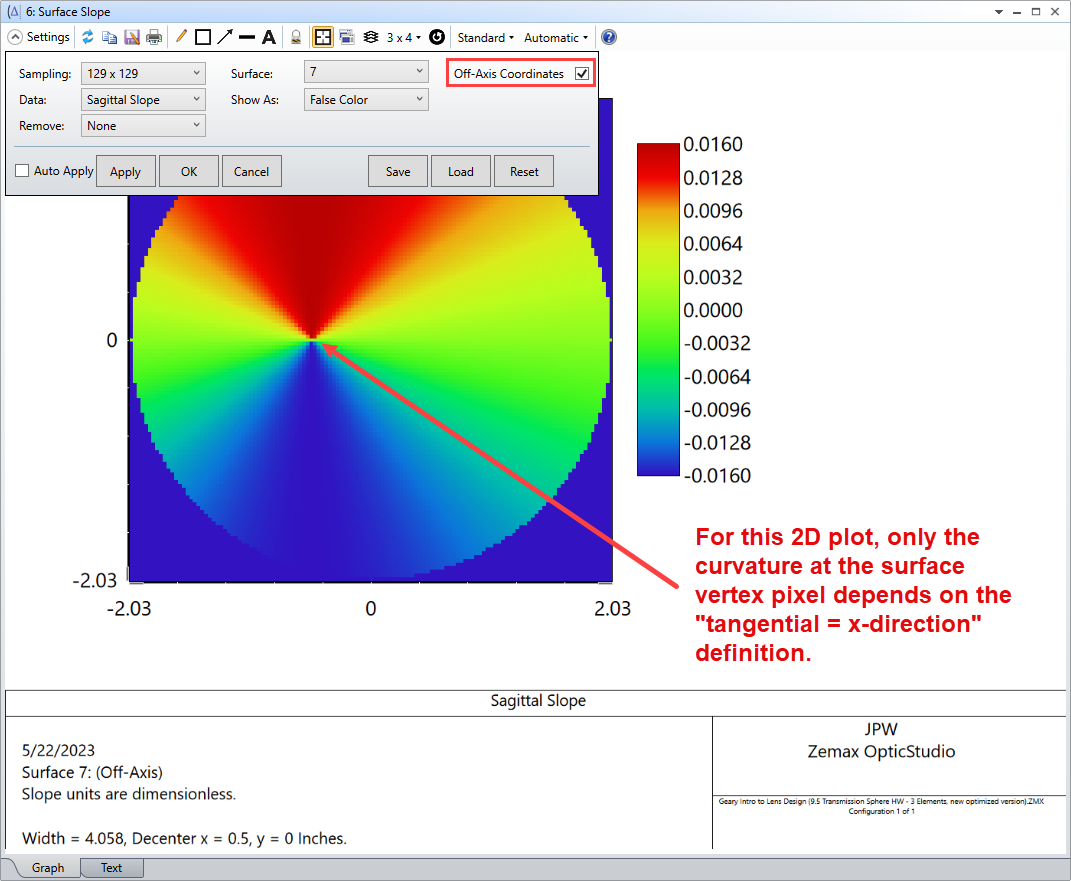
I must admit I assumed that this was the case in the curvature plots. I read the documentation, and it’s not described there. I searched for a KB article instead and found what I needed to correct my understanding. But since the convention is arbitrary, did we have to use a convention that is orthogonal to the convention used elsewhere?
This is an old feature and I know that changing the convention will be problematic for backwards compatibility, -and I also know whose watch this decision was made on - but maybe the documentation, rather than a KB article, could point out the difference in convention?
Mark
Page 1 / 1
Hey Mark,
Thanks for catching this. I’ve always been confused by this notation so I rarely use Tangential + Sagittal. As you mentioned, in all other areas of OpticStudio, we always write “Tangential and Sagittal” with tangential always talking about the +y axis. My best guess is that Zemax chose tangential to be tangent to radial zones.
I would argue that Zemax should break compatibility and swap the 2 values. As you mentioned, this choice is arbitrary but if you think about, to get a cross-section (which these plots are), you have to “scan” across the surface. Tangential (tangent) as the name implies, should be tangent to this scan direction:
This also aligns with the traditional “bike wheel” concept for astigmatism, namely that the tangent direction is tangential to the spoke (and spoke = sagittal...both start with “s” so easy to remember ):
Although it’s minor, I would argue that the definitions are wrong (even though they’re arbitrary) and should be swapped & documented as a bug report. However, I doubt the analysis will be updated so hopefully I can remember this is one of the quirks of OpticStudio.
Hi Mark,
I’m trying to understand your concern. I took a fresh look at Shawn’s KB article, which I read initially some time ago. It’s very helpful, and some portion of it should really be included in the help documentation. In any event, since surface curvature depends on the direction in which the curvature is measured, a convention regarding direction must be adopted.
As Shawn notes:
It seems fine, and indeed appropriate, to take the tangential direction along a radial direction. When considering a 2D plot of surface curvature, the only point which is ambiguous is the surface vertex, so for this one central point the tangential direction is taken to be the x-direction:
Now I agree that taking the y-direction might have been the better option, but this choice only affects the central surface vertex point for a 2D plot (in other words, it’s a single-pixel issue).
For a 1D curvature cross section, the ambiguity disappears as the tangential direction is always defined to be along the axis of interest:
Even for 2D curvature plots, when considering radially symmetric surfaces that are centered on the optical axis, it doesn’t really matter what the convention is because the curvature value at the surface vertex is the same for all radial directions. It’s only for non-radially-symmetric surfaces or radially-symmetric surfaces with a decentered aperture (and the “Off-Axis Coordinates” option on the curvature plot is selected) that the tangential-direction convention comes into play -- but again this only affects the curvature value at one point. For example, here is a spherical surface with a decentered aperture:
So, in the grand scheme of things, it doesn’t seem to me that the current convention is that big of an issue. Am I missing something?
Regards,
Jeff
No, you’re not missing anything. I just assumed the convention was the other way round. The kb article is totally correct, but I just didn’t expect the convention to be that way round
Got it. Yes, I agree, practicing uniform consistency with conventions would be a good thing.
- but maybe the documentation, rather than a KB article, could point out the difference in convention? 
