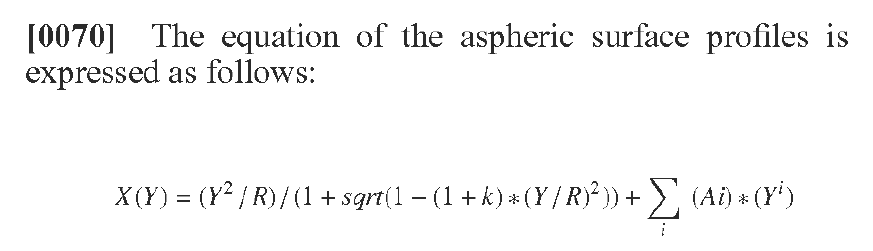Dear Optics Experts,
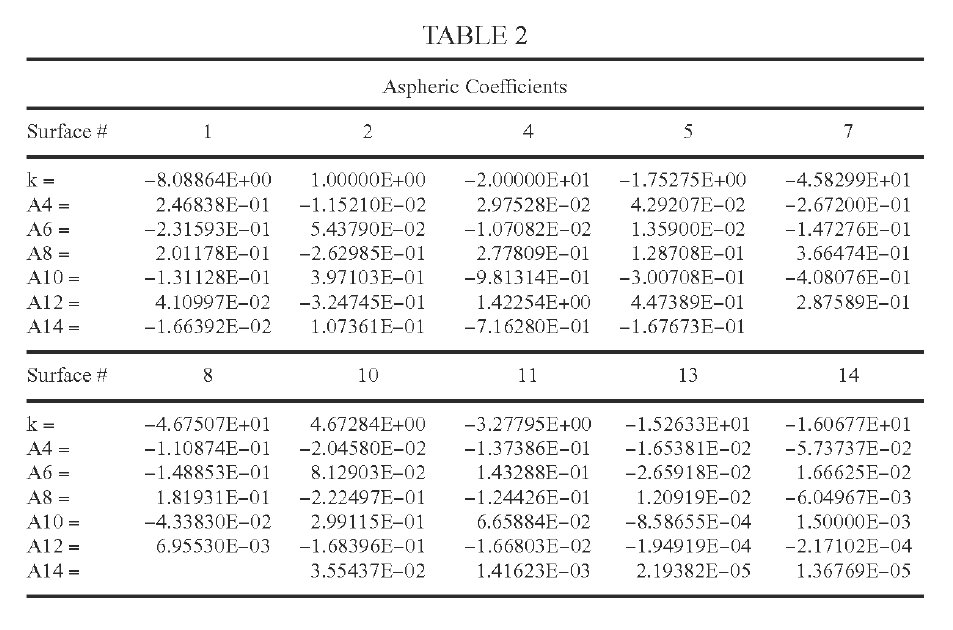
while manufacturing an aspheric lens, I wondered why Zemax has the second order term, i.e. the r^2 term, in the aspheric surfaces, which is also in the help pdf? Other definitions of aspheric surfaces leave out the r^2 term, which seems to make sense to me, as the r^2 term seems to closely interfere with the spherical radius. This becomes then a bit confusing also towards the manufacturers. Is there an advice when to use this 2nd order term in aspheric optimization? Also when to use a (or only a) conic term?
Also the tool Best Asphere does not use the 2nd order term.
Thanks you for the advice!
Markus