I have a model of a lens and want to look at the focal power at different field angles. I don't fully understand how the normalized field coordinates work for e.g. diagonal fields.
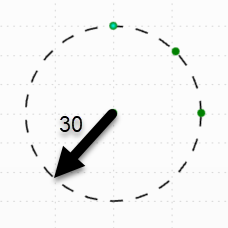
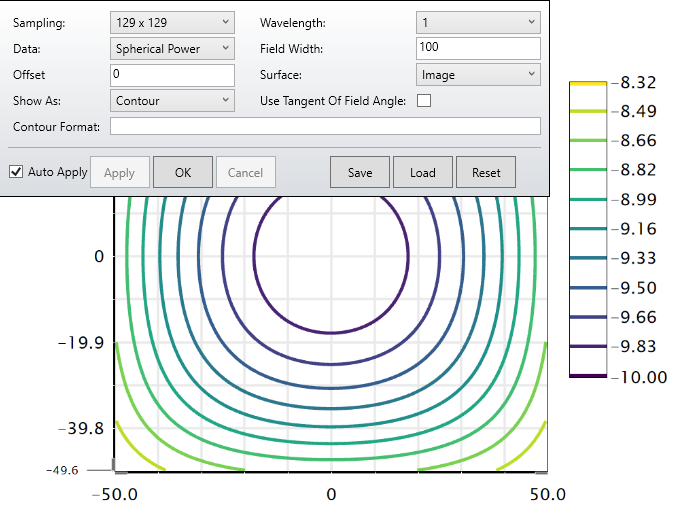
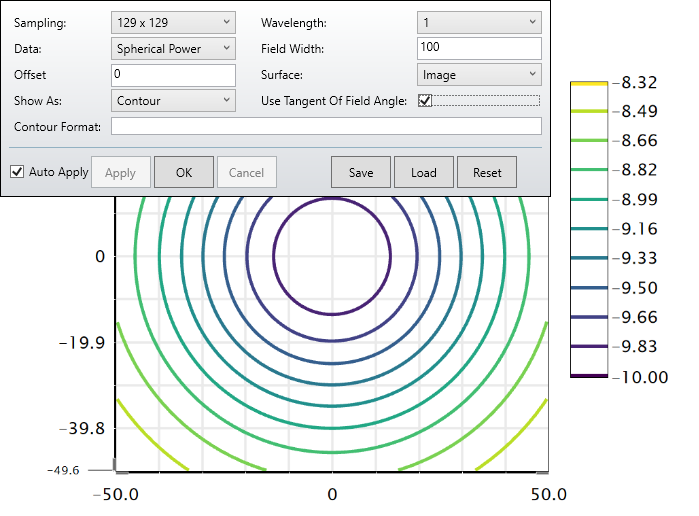
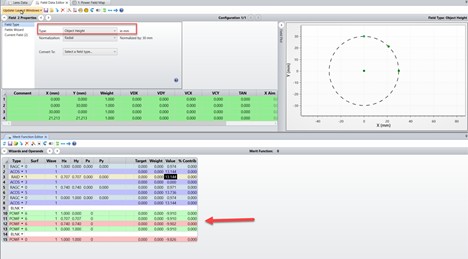
In the attachment, I have a simplified version with a spherical lens to illustrate the issue that I am seeing. I created 3 fields in the field data editor: (0°, 30°), (30°, 0°), (21.213°, 21.213°). The last field is a diagonal field coordinate with the amplitude 30° (30°/SQRT(2)=21.213°). I expect the focal power in each of the three field points to be identical, since the lens is rotationally symmetric. Indeed, the Power Field Map tool the contour lines for a fixed focal power seem to be circles.
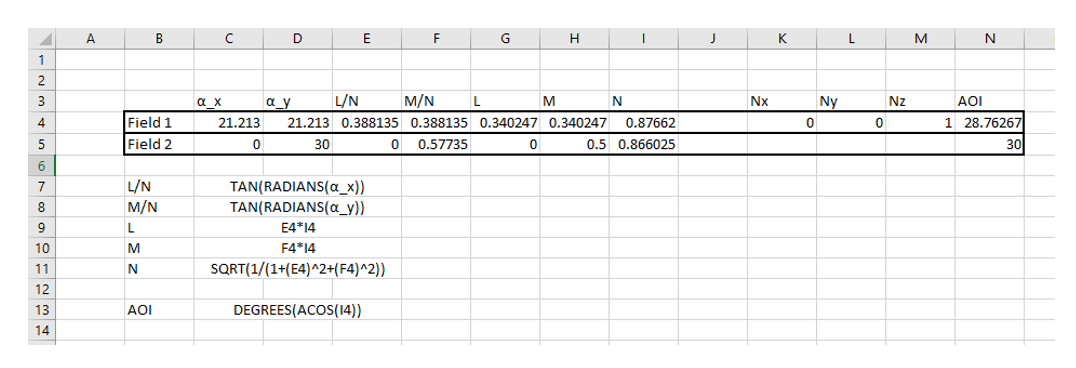
However, next I evaluate the focal power for the different field points in the Merit Function. It turns out that at the normalized field coordinates (1, 0) and (0, 1), I get a focal power of -9.524 dpt. But at (0.707, 0.707), I get -9.563 dpt. To get to the same focal power that I get on axis, I need to pick the field coordinates (0.740, 0.740).
Also if I evaluate the field angle from the ray data (ACOS(RAGC)), the norm. field coordinate of (0.707, 0.707) gives 28.763°, instead of 30°.
Can someone explain to me why for the diagonal fields, the field amplitude is different? How do I calculate the field coordinate that is equivalent to (1, 0), but turned by 45°? What does the Power Field Map tool actually plot on the x and y axis - is it maximum field * normalized field coordinate?




 (Plot is from wikipedia:
(Plot is from wikipedia: