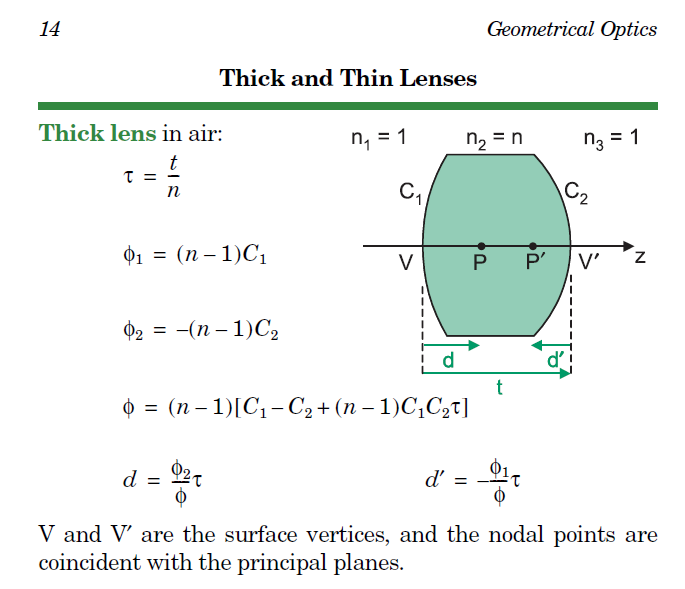
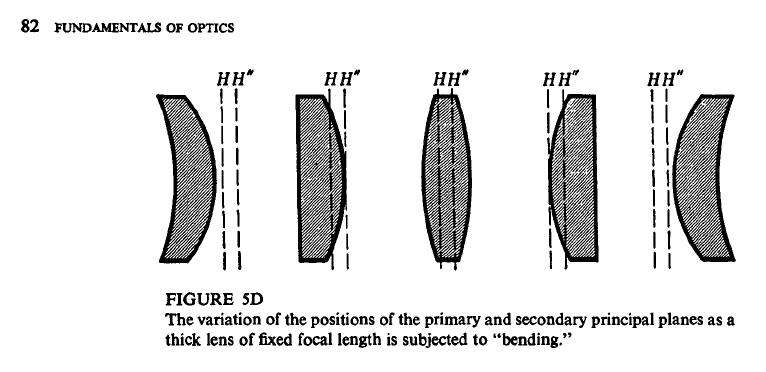
From reading this interesting discussion below.
I went down a rabbit hole when I was figuring out where the object principal plane of a thick plano-convex lens is. I’ve been taught to find the principal planes like its described at RP Photonics, that is:
extrapolate the ingoing and outgoing rays such that they meet in a plane
However, when rays parallel to the optical axis enter through the plane face of the lens, the ingoing and outgoing rays will meet exactly along the convex face, which is not a plane.
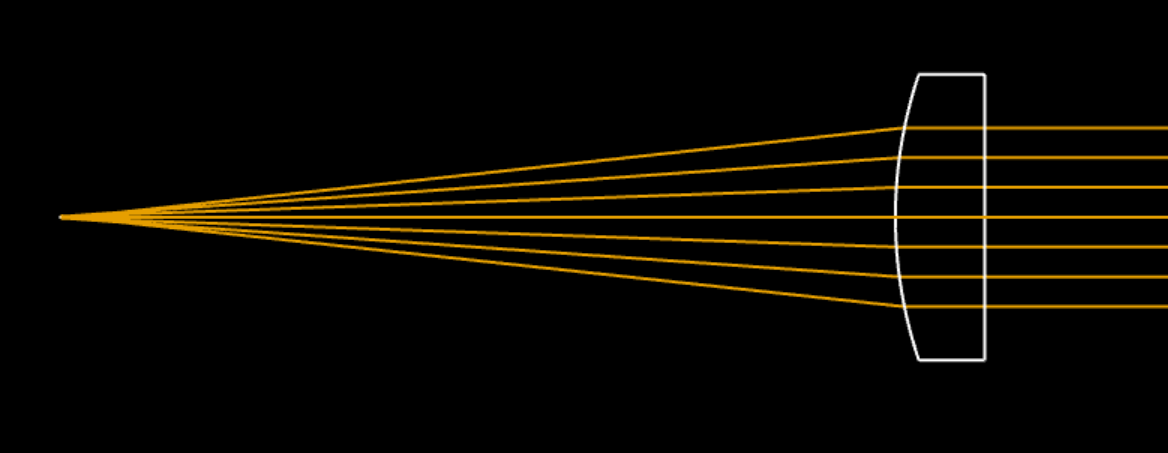
Therefore, I believe the principal plane is defined as the plane coincident with the convex surface vertex. At least, this is what I’ve taken away when I used OpticStudio (surface 1 is the convex surface).

I also found this information here:
Plano-convex and plano-concave lenses have one principal plane that intersects the optical axis, at the edge of the curved surface, and the other plane buried inside the glass.
I can accept this definition, but I was curious, from a teaching perspective, to hear if someone can provide an explanation that would be compatible with the “traditional” explanation: find the plane where the in and out rays bend. I know we are at a boundary between paraxial and real optics and it might not make sense to ask this question, but I could imagine a student asking about this and all I could answer for now is that in this instance we choose the vertex of the convex surface as the principal plane and its a special case.
Take care all,
David